论文笔记：Batch Normalization

参考论文：
Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift

Abstract

Internal Covariate Shift：
在深度网络的训练期间，由于网络参数变化而引起的网络激活（网络内部结点）分布的变化。

ICS导致的问题：

深层网络训练时，由于模型参数在不断修改，所以各层的输入的概率分布在不断变化，所以须使用较小的学习率及较好的权重初值，导致训练很慢，同时也导致使用saturating nonlinearities 激活函数（如sigmoid，正负两边都会饱和）时训练很困难。

解决办法是：Batch Normalization

BN是： 使正则化层称为模型结构的一部分，在训练每个mini_batch时，单独进行Normalization 。

BN的好处： 让我们可以使用更大的学习率，初值可以更随意；它起到了正则项的作用，在某些情况下，有它就不需要使用Dropout了。

在Imagenet上， achieves the same accuracy with 14 times fewertraining steps

Introduction

随机梯度下降（SGD）已被证明是训练深度网络的一种有效方式，而动量）和Adagrad等SGD的变体也取得了非常好的效果。下文以SGD为例进行讨论。

SGD遇到的问题

SGD目标

$$\theta=\underset{\theta}{\arg\min}\frac{1}{N}\sum_{i=1}^N\ell(x_i,\theta)$$

用mini_batch去近似整个训练集的梯度

$$\frac{1}{m}\frac{\partial\ell(x_i,\theta)}{\partial\theta}$$

（在并行计算下，m个合成一个batch计算比单独计算m次快很多；且用m个样本去估计整个训练集的梯度方向比用单个样本要准确。所以用一个mini_batch下降一次要比用一个样本下降mini_batch次要好。）

虽然SGD简单高效，但它需要调整模型超参数，特别是优化中使用的学习速率以及模型参数的初始值。每个层的输入都受到前面所有层的参数的影响，因此随着网络变得更深，网络参数的微小变化就会放大。

这就带来一个问题：各层输入分布的变动导致模型需要不停地去拟合新的分布。

Covariate Shift扩展到子网络

当学习系统的输入分布发生变化时，会发生协变量变化（Covariate Shift）

当一个学习系统的输入分布是变化的时（即训练集的样本分布和测试集的样本分布不一致），训练的模型就很难有较好的泛化能力，这叫做covariate shift (Shimodaira, 2000)，解决办法是domain adaptation (Jiang, 2008).和迁移学习。

然而，协变变化的概念可以扩展到整个学习系统中，适用于其子部分，如子网络或层。考虑一个网络计算

整个network损失函数为：

$$\ell=F_2(F_1(\mu,\theta_1), \theta_2)$$

学习$\theta_2$可以看作是输入$F_1(\mu,\theta_1)$被送入子网络
sub-network的损失函数为：

$$\ell=F_2(x, \theta_2)$$

sub-network的SGD（$m$是batch_size，$\alpha$是学习率）：

$$\theta_2\leftarrow\theta_2-\frac{\alpha}{m}\frac{\partial{F}_2(x_i,\theta_2)}{\partial\theta_2}$$

这与具有输入$x$的独立网络$F_2$完全等效。

因此，使训练更有效的输入分布特性，也适用于对子网络进行训练。
将Covariate Shift扩展到子网络，即我们想要每个sub-network的输入分布都不要有太大的变化，这就引出了Batch Normalization的方法

BN希望通过对每个子网络输入的归一化，来对子网络的输入分布进行一定程度的fixed。

Towards Reducing Internal Covariate Shift

Internal Covariate Shift 算是将Covariate Shift扩展到每一个子网络的一个说法。希望每个子网络的输入都不要有太大的变化（在深度网络中，前一层一个参数的微小变化对于深层参数可能产生较大的影响）。

Batch Normalization就是为了降低Internal Covariate Shift。

算法思想

前面提到BN是想，在每次mini_batch的数据进行训练时，每一层的输入都进行归一化（子网络的思想就是：每个子网络的输入都进行处理）。

$$\hat{x}^{(k)}=\frac{x^{(k)}-E(x^{(k)})}{\sqrt{Var(x^{(k)})}}$$

但是，简单地标准化每层的输入可能会改变该层可以表示的内容。例如，Sigmoid函数虽为一个非线性的函数，通过Normalization可能将输入压缩到其线性部分。

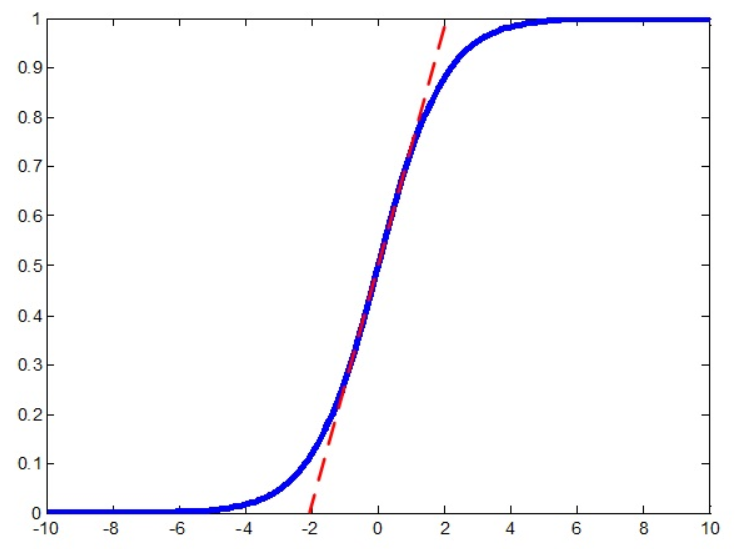
我们希望，可以灵活地学习压缩范围，比如压缩到$[-5,5]$等某个更适合拟合训练集的某个区间。

所以针对每个层的激活引入了一对参数，使压缩区间可以移动和放缩：

$$y^{(k)}=\gamma^{(k)}\hat{x}^{(k)}+\beta^{(k)}$$

其中$\gamma$和$\beta$可在训练中学得。

并且，当$\gamma^{(k)}=\sqrt{Var(x^())}$，$\beta^{(k)}=E(x^{(k)})$可还原出原先的分布。所以，这种拟合效果至少不会比原先的表示差！

forward

只要minibatch中的样本采样与同一分布，规范化后的输入 x 期望为0，方差为1，把规范后的 x 进行线性变换得到 y 作为后续层的输入，可以发现 后续层的输入具有固定的均值和方差的。尽管 规范化后的 x 的联合分布在训练过程中会改变(源于第一个简化，本文的规范化是把 x 向量中各个变量当作独立的，单独规范化的，所以他们的联合分布并不稳定，只是单独是稳定的)，但还是可以使训练加速。

backward

优化中也需要对BN的两个参数进行优化，链式法则求导就可以了：

具体推导可参见

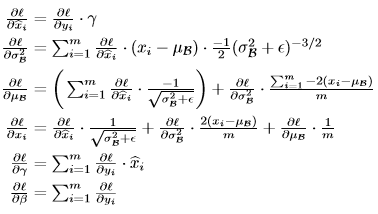
BN是可微的，通过BN变换，可以减弱输入分布的 internal covariate shift ，并且学习到这个线性变换与网络本来的变换是等价的。

其他几个问题总结

Batch Normalization的好处

• 保持各层输入的均值和方差稳定，来减弱 internal covariate shift；
• 也让梯度受参数及其初值的减小；
• BN也算作正则项，减少对Dropout的依赖；
• 它让卡在饱和区域的概率降低，以便可以使用 saturating nonlinearities（如Sigmoid，tanh等激活函数）

BN层的位置

原本按照BN的思想，当在每一层的激活函数之后。例如$ReLU=\max(Wx+b,0)$之后，对数据进行归一化。然而，文章中说这样做在训练初期，分界面还在剧烈变化时，计算出的参数不稳定，所以退而求其次，在$Wx+b$之后进行归一化。因为初始的$W$是从标准高斯分布中采样得到的，而$W$中元素的数量远大于$x$，$Wx+b$每维的均值本身就接近0、方差接近1，所以在$Wx+b$后使用Batch Normalization能得到更稳定的结果。

实验

实验和梯度推导可参见